HTHCV Flagpole Problem
Problem Statement
In the front of High Tech High Chula Vista we have a flagpole standing at tall height. We are learning about measurement currently and we looked at the flag pole and saw that finding the estimate of that can really test our ability of how wee been learning to measure. So we took on the task of using the three methods we learned, shadow method, isosceles triangle method, and mirror method, and saw what we can accomplish.
The questions we took on with this problem were:
What was your initial guess for the height of the flagpole before we took any measurements?
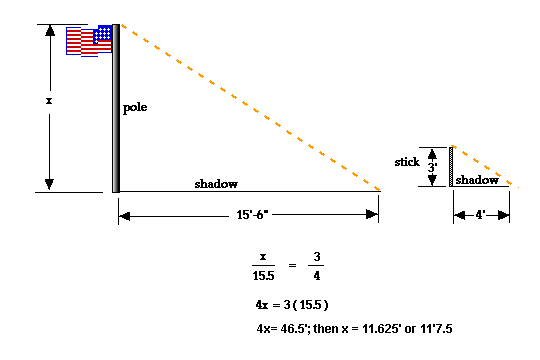
What was your estimation using the shadow method?
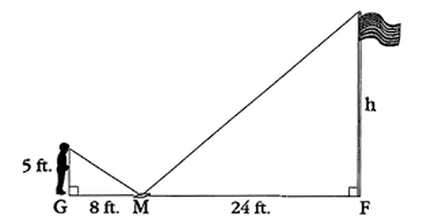
What was your estimation using the mirror method?
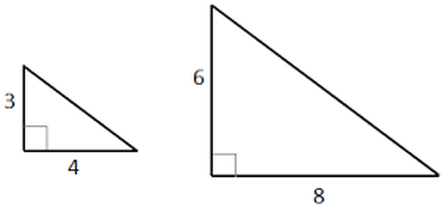
What was your estimation using the isosceles triangle method?
The questions we took on with this problem were:
What was your initial guess for the height of the flagpole before we took any measurements?
What was your estimation using the shadow method?
What was your estimation using the mirror method?
What was your estimation using the isosceles triangle method?
Process & Solution
We started this problem by taking time out of our class time to go and examine the flagpole. When we out there, we all tried to guess what the height was just by looking at it. Then we came up with the method of let someone stand next to and compare their height to the flagpole's height. We tried to see how many of that person could fit into the flagpole's height. It was a start, but obviously it wasn't a very accurate estimate. My initial guess for the height of the flagpole was minimum 50 feet and maximum 75 feet. This whole problem revolved around similarity and similarity problems. When two shapes are similar is when the ratios of their lengths are corresponding to each other.